Snowflakes
:date: 2023-10-19 20:19 :tags:
I wanted some snowflakes for an art project and so I wrote a program to generate simple snowflakes.

There is a surprising amount of complexity in the construction of these. They are also squished oblong to simulate an oblique view, and rotated and even skewed a tiny bit for some subtle perspective. Yes, my artistic style could be described as "nerd overkill".
The next problem was that I really wanted a big collection of these. Unfortunately my nerd overkill sensibilities had me prematurely worrying that the result would look exactly like this.

This composition places the snowflakes randomly. They could find themselves anywhere. Is that technically correct? Is that artistically pleasant? I don't know. What I was afraid of is that if you do things randomly you often get clumps. For example, here are 100 lines of 100 characters and about 8.4% of the lines contain clumps of 4 (or more) repeating digits.
$ for i in $(seq 100);do tr -dc '0-9'</dev/urandom|head -c 100; echo; done|grep -E '(.)\1{3}'
6360127793006048114297380849526666988585556392057407959484793954154670481588947940184825261235595270
6136184745366894797281775073879106743945270286411335191906140130082694013169496500008257500343258359
0326235771907933182320172681884121586388161242857529652252984248453333719713828951327390875111065690
5835631290935883894467680186677800647300519527703201228009855394600000459412695584141279372327639853
4562959055456587186072062204577767644263516789361892176713867356698353831838244533333316667656465586
3983153910565141608266259731649390968802702476675499351025888882697351838658057646896637687759978028You might think, well, that's how "random" rolls. You get what you get. But sometimes, especially for art projects, hardcore random is just not ideal.
The idea I had to fix this (completely made up) problem was to draw inspiration from an interesting source of randomness explained nicely by Stephen Wolfram's book "A New Kind Of Science" — nicely gifted to you at this web site: wolframscience.com/nks. If you read just one page from this book I would recommend — page 27 which introduces the idea of how very simple rules can produce quite a lot of complex behavior. Or just look at this figure from that page.

These patterns take simple rules and produce complex output. If you start with some random input and apply the rule, you can get very complex patterns. Are these "random"? Well, that's hard to say. While columns of values pulled off of these diagrams could pass a lot of tests for "randomness", they're clearly the product of very simple deterministic rules. But they sure look interesting. Wolfram believes a lot of patterns in nature use rules like this and even, sometimes, this exact kind of rule. Here, for example, is a seashell that seems to have the exact Rule 30 pattern on it.

But for my purposes, I remembered these diagrams as having patterns that were definitely random-like and that neatly filled a plane. Well, some rules did.
By design it should be easy to write these rules into software and that's what I did. I generated the patterns for some well known rules that produce "interesting" behavior. I then checked for diagonal runs (to the upper left) and if the run was long enough I placed a snowflake there. If it was small, I put a circle.
Note that I did a little jiggling of pretty much everything so it will be hard to see exactly what my algorithm was but you can get an idea.

This first one shows no flakes because Rule 110 creates shapes that don't have diagonal runs that go up and to the left. But you can see it creates a kind of structure and I'm using that structure. This rule actually can make interesting patterns if you turn it 45 degrees when you're done — but that was not quite worth actually doing in my project. (Yes, even I have limits.)
Rule 30 is one of the more interesting rules. While it makes a neat looking structure, it's not quite what I'm after in the distribution.

You can see how I'm placing the flakes in the corners of the negative space "shapes" (sort of). This shows the idea pretty well, but it's not quite right.

Rule 90 is not bad. Really any of these can be tweaked to work but this wasn't the best for my applications.
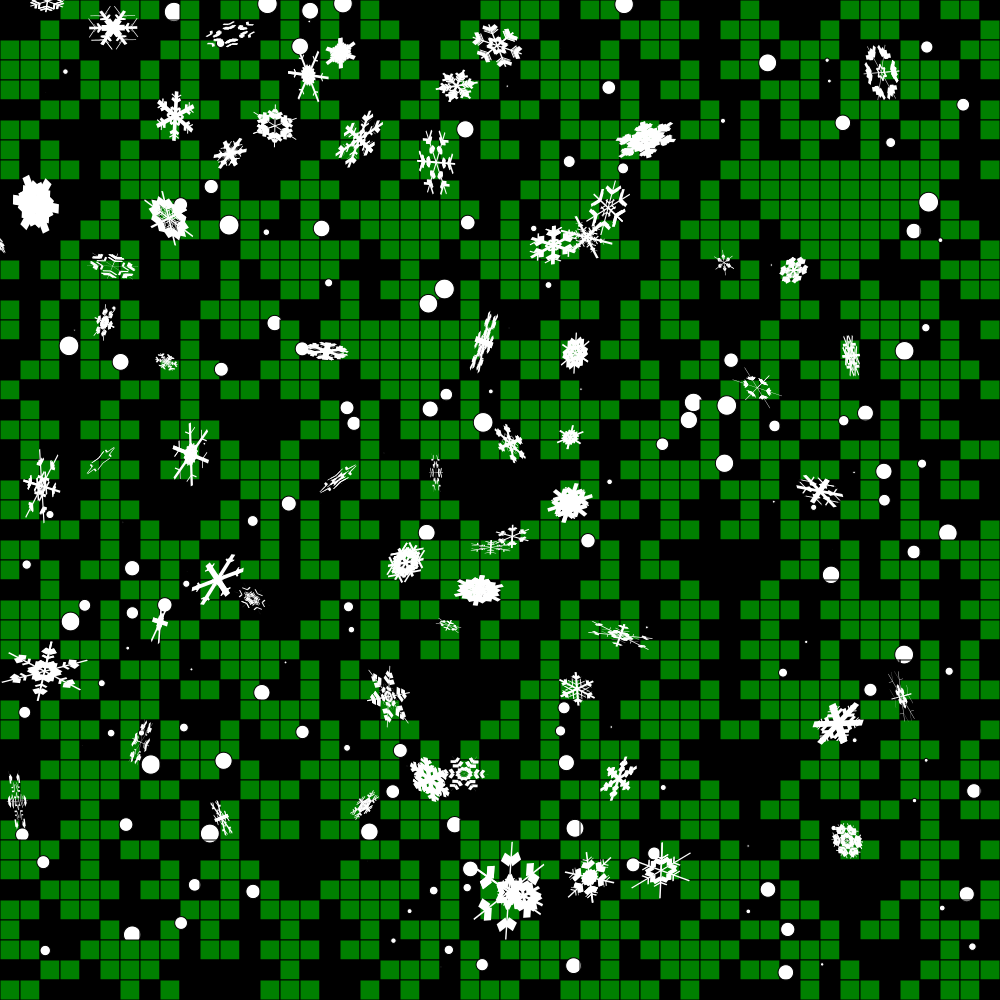
Rule 150 shows everything working better and is pretty decent but it can be improved.
Finally we get to Rule 165. I'm a bit surprised based on the pattern of the cellular automaton but it does seem to distribute the flakes quite nicely. No serious clumps. All the space pretty well used. Definitely random-ish.

Although that's not perfect it is close enough to what I want. Here is a sample of the scene based on Rule 165. There are a few clumps but most of the space is used and it's a lot less clumpy than pure random.

I am aware that there are other ways to achieve an effect like this. Blender has very good noise modifiers for filling a plane with aesthetically pleasing "random" patterns. For example, Voronoi texture and Musgrave texture (using Perlin noise). But since I was not using Blender but rather writing everything from scratch, it seemed reasonable to take these very simple Wolfram rules for a spin.
I can't say that I recommend this level of nerd overkill for anything other than indulging in wanton nerdiness. This was an interesting exploration of the aesthetic possibilities of these automata but mostly I was just having fun with neat computer generated images.