Graph Theory Resources
-
A nice review of graph theory for the purposes of Python programming. This includes a simple but sensible graph class.
Path Planning
-
Another approach involves hubs (one is called "Hub Labels") and uses precomputed tables to speed things up. This is useful for road route planning. Here is a paper on the topic. This may be related to contraction hierarchies. Contraction hierarchies seem to be about caching shortcut calculations.
-
A good resource from Stanford including sample implementations of A* and good explanations.
Graphviz
Graphviz Resources
-
A great resource for getting started with Graphviz including excellent simple examples.
-
A nice O’Reilly article about Graphviz.
Output Formats
-
-Tps -
-Tpng -
-Tsvg
Digraph
strict is if only one edge between nodes is allowed.
// Sample Family Tree
strict digraph {
{maryellen;carlos} -> carlosjr
{winifred;carlosjr} -> {margaret;robert}
{albert;gertrude} -> {winifred;olive;derek;jean}
}Process with this command.
dot -Tpng familytree.dot -o familytree.pngWhich should produce something like this.
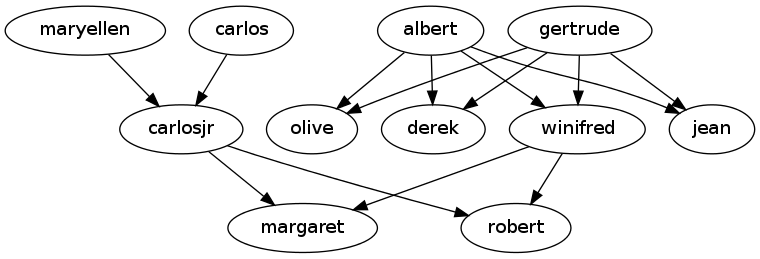
Here’s another example.
digraph { label="Enchanting Requirements";
string[color="red"];
diamond[color="red"];
cane[color="red"];
iron[color="red"];
obsidian[color="red"];
cows[color="red"];
log[color="red"];
redstone_dust[color="red"];
lapis[color="red"];
grass[color="red"];
coal[color="red"];
furnace->iron;
coal->iron;
iron_pick->lapis;
iron->iron_3_bucket;
iron->iron_3_iron_pick;
log->stick_2_iron_pick;
stick_2_iron_pick->iron_pick;
iron_3_iron_pick->iron_pick;
string->string_3;
string_3->bow;
log->stick_3_bow;
stick_3_bow->bow;
iron_3_bucket->bucket;
bucket->water_bucket;
iron_pick->redstone_dust;
redstone_dust->dispenser;
bow->dispenser;
water_bucket->dispenser;
dispenser->cow_farm;
log->fence_post;
log->button;
grass->seeds;
seeds->wheat;
log->stick_2_hoe;
stick_2_hoe->hoe;
hoe->wheat;
iron->iron_5_hopper;
iron_5_hopper->hopper;
chest->hopper;
log->chest;
chest->cow_farm;
fence_post->cow_farm;
button->cow_farm;
wheat->cows;
cows->cow_farm;
hopper->cow_farm;
iron_pick->diamond;
diamond->diamond_2;
diamond->diamond_3;
diamond_2->enchant_table;
log->stick_2_diamond_pick;
stick_2_diamond_pick->diamond_pick;
diamond_3->diamond_pick;
cow_farm->leather_46;
leather_46->book_46;
cane->cane_414;
cane_414->book_46;
log->log_23;
log_23->wood_90;
wood_90->bookshelf_15
book_46->bookshelf_15
lava->obsidian;
bucket->obsidian;
diamond_pick->obsidian;
obsidian->obsidian_4;
obsidian_4->enchant_table;
book_46->enchant_table;
lapis->enchant_setup;
enchant_table->enchant_setup;
bookshelf_15->enchant_setup;
}

RT Graph 3D
If Graphviz isn’t quite right because your graphs are really very 3 dimensional, "RTgraph3D will let you create dynamic graphs in 3D." One potential application of this is molecules. I haven’t tried it out myself but it’s worth noting.
Jargon
There sure are a lot of terms of art that need very careful definition. Here are many of them in one place.
- graph
-
Set of edges and a set of vertices and a function that relates them.
- simple graph
-
No loop backs or multiple edges. Also called "multigraph". Generally finite number of edges and vertices.
- cycle graph
-
n edges and n vertices. Imagine a circle approximated by points along it (though there are other uglier ways to plot it).
- adjacent vertices
-
When there is an edge connecting a pair.
- adjacent edge
-
Have at least one vertex in common.
- incident
-
e is incident to v and w if v and w are connected by e. Also v and w are incident to e in that case.
- degree of vertex
-
Number of edges which are incident to it. A loop counts as 2. A.k.a. "valency" in chemical structures (carbon=4, hydrogen=1).
- n-regular
-
A graph where every vertex has the same degree, n.
- null graph
-
Edge set is empty.
- complete graph
-
Every pair of distinct vertices is joined by an edge. Represented as Kn where there are n edges connecting all of n vertices to each other.
- bipartite graph
-
The vertices are divided into 2 sets and every edge goes from one set to the other.
- complete bipartite graph
-
A bipartite graph where every vertex of set 1 is connected to every vertex of set 2.
- adjacency matrix
-
A computer-friendly representation of a graph as a
n`x`nmatrix such thata~ij~is the number of edges connecting verticesiandj. It’s possible that this could alternatively mean a matrix populated with a 1 or 0 depending on if there is a connection. This is true by default in a "complete graph". - isolated vertex
-
No edges connect to it.
- connected
-
If any vertex can reach any other. No islands basically.
- path
-
An edge traversal sequence where all traversed edges are distinct. Vertices can be revisited. Not all vertices or edges of a graph need participate for there to be a path.
- simple path
-
A path where the vertices (with the possible exception of the first and last) are also distinct, i.e. visited only once.
- closed path
-
V0 = Vn , i.e. the beginning vertex and end vertex is the same.
- cycle
-
A.k.a. curcuit. A closed simple path containing at least one edge.
- Eulerian path
-
A closed path which includes every edge.
- Eulerian graph
-
A graph which contains at least one Eulerian path. A connected graph is Eulerian if and only if every vertex has an even degree. Hence there is no solution to Koenigsberg Bridge quandary.
- Hamiltonian cycle
-
A cycle which passes through every vertex. Complete necessary and sufficient conditions for a graph to be Hamiltonian are an unsolved problem. However, a sufficient condition is if the number of vertices, n, is >= 3 and the degree is >= .5*n, then the graph is Hamiltonian. A graph can still be Hamiltonian without satisfying this theorem.
- isomorphism
-
When two graphs share the same essential structure even if that structure is enumerated differently. Are all the things possible (routes) in one graph possible in the other? Isomorphic. To demonstrate isomorphic relationship, an isomorphism must be found (necessary and sufficient). To show they are not isomorphic, any of the graph theory properties (number of vertices/edges, degree, simple, Eulerian, Hamiltonian) shown to not match is sufficient. In chemistry a structural isomer is a different graph of the same edges (atoms); these are not isomorphic.
- tree
-
A connected graph containing no cycles.
- spanning tree
-
In a graph with vertex set V, a subgraph which is a tree and also has a vertex set V (all of them, no cycles).
- minimum spanning tree
-
A spanning tree which is the smallest possible (total edge lengths).
- Steiner tree
-
Similar to a minimum spanning tree but with the possibility of adding additional nodes not part of the original set of nodes.
- full binary tree
-
One vertex has degree 2 (top or root node) and all other vertices have degree 3 (branch or decision nodes) or 1 (leaf nodes). There are always 2 or more leaf nodes than decision nodes.
- level
-
Level of a vertex in a tree is the length of the path jointing that vertex and the root vertex. The level of the tree is the maximum level of all vertices in a tree.
- bridge
-
Edge that will divide a graph into two graphs if removed.